p13x13t: Unveiling the Concept, Applications, and Future Potential

In the world of emerging technologies and new frameworks, p13x13t is an intriguing term that invites curiosity. What does it mean? Where might it apply? How could one use it in practical systems? In this article, you will find a full exploration of p13x13t its possible definitions, design principles, use cases, benefits, challenges, and tips for implementing it in real applications.

Introduction: What Is p13x13t?

The notation p13x13t suggests a structured, possibly matrix-based or grid-based concept, with the “13×13” part reminiscent of a 13 by 13 dimension and the “t” perhaps indicating a transform, tensor, or temporal dimension. But p13x13t is not just about a 13×13 grid it embodies a philosophy: balancing dimensional richness with operational simplicity.

In this article, we dive deep into what p13x13t might represent in data systems, algorithm design, graphics, or advanced computational frameworks. We analyze its architecture, possible applications, performance implications, security aspects, and how you might adopt it in your projects. Throughout the article, you will see the term “p13x13t” repeatedly, because it is our anchor concept.

Origins & Theoretical Basis of p13x13t

Since p13x13t is not yet mainstream, we begin with plausible theoretical foundations:

1. Dimensional Matrix Foundation

The “13×13” suggests that p13x13t is based on a two-dimensional square matrix of size 13 in each direction.
The “p” could stand for “projection”, “pattern”, “processing”, or “parameterized”.
The trailing “t” might mean “transform”, “tensor”, “time”, or “transpose”.

Thus, one might interpret p13x13t as a parameterized 13×13 transform matrix, or a projection tensor of dimension 13×13 over time, or a pattern-driven 13×13 data block with transformations.

2. Tradeoff Between Manageability and Richness

Why 13×13? Why not 16×16 or 8×8? The choice of 13 as a prime dimension gives certain mathematical advantages:

Prime dimension helps in avoiding trivial divisibility, which can reduce symmetries that complicate certain transformations.
13×13 gives 169 cells, a moderate size for many computational operations (not too large to overwhelm memory, but large enough to encode complexity).
The “t” dimension could allow layering over time or multiple states.

Hence, p13x13t can be a unit block in a larger system, offering both complexity and structure.

3. Extensions to Higher Order

One can generalize: pN×Nt, where N = 13 is a special, chosen dimension. But p13x13t is a focus case because its dimension is small enough for fast operations but large enough for expressive data encoding.

Core Architecture: Structure of p13x13t

To understand p13x13t, let’s break down its core architecture, which you might adopt in system design:

Grid / Matrix Layer

At the base lies a 13×13 grid (matrix). Each cell in this grid holds a data value (scalar or vector).
The grid may be dense (all cells filled) or sparse (many zeros or nulls).

Transform / Temporal Layer (“t”)

The “t” dimension could represent time i.e., a sequence of 13×13 snapshots.
Alternatively, “t” might represent transform layers (e.g. frequency domain transforms).
In a temporal interpretation, you might have p13x13t[0], p13x13t[1], … p13x13t[T-1].

Parameterization (“p”)

The “p” indicates that the structure is parameterized meaning you can scale, warp, or configure how the grid evolves or transforms.
Parameters may include weights, scaling factors, boundary conditions, coupling between grid cells, etc.

Interfaces & APIs

To integrate p13x13t in software, you define APIs to read, write, transform, and query the grid at different time slices.
You might support interpolation between time layers, compression of grid states, or combining multiple p13x13t blocks.

Hierarchical Composition

Many systems may not use a single p13x13t block. Instead, you can cascade or tile multiple p13x13t units to form larger structures.
For example, a 3×3 tiling of p13x13t blocks yields an effective 39×39 grid (core composition).

Potential Applications & Use Cases for p13x13t

Though p13x13t is a conceptual framework, here are some areas where it could find real utility.

1. Image & Signal Processing

Image patches: Many image algorithms operate on small patches (e.g., 8×8, 16×16). A 13×13 patch is a nonstandard size but could be used for specialized filtering or feature maps.
Transform basis: p13x13t could act as a transform block (like discrete cosine transform) for image or signal compression.
Video frames: With “t” as time, p13x13t could represent a stack of 13×13 frames (mini video cubes), useful for lightweight tracking.

2. Neural Networks & ML

Embedded representation: In a neural network layer, each neuron might produce a 13×13 map. p13x13t becomes a hidden tensor shape.
Attention cubes: A 13×13 attention map evolving over time (t) can represent dynamic relationships in sequence models.

3. Data Grids & Sensor Networks

Sensor grids: Suppose a grid of 13×13 sensors collects data at discrete time intervals. You get a p13x13t data cube. One can apply analysis, anomaly detection, or interpolation.
Spatial-temporal modeling: p13x13t can serve as the base unit in spatio-temporal models, e.g. environmental data on a small grid across time.

4. Cryptography & Steganography

Block cipher units: p13x13t could define a block size in an encryption scheme, mixing and transforming blocks over time.
Data embedding: The 169 cells can hold concealed information; the “t” dimension allows multi-layer embedding across time or versions.

5. Game Design & Procedural Generation

Tile maps: A game world may use a 13×13 tile map evolving over time (weather, growth), so p13x13t is a natural representation.
Pattern evolution: Cellular automata on a 13×13 grid evolving over t steps.

Benefits & Strengths of p13x13t

Why might someone choose p13x13t over simpler or more conventional structures? Here are its primary advantages:

Balanced Complexity

13×13 is small enough to be computationally tractable, yet large enough to represent interesting patterns.
It avoids trivial symmetric decomposition (because 13 is prime) in many algorithmic contexts.

Temporal or Transform Layer

The extra “t” dimension allows dynamic behavior, making p13x13t richer than static matrices.
It supports evolution, history, or transform-based analysis (e.g. frequency/time domain).

Modularity & Composability

p13x13t blocks are modular and can tile or stack to build larger systems.
You can build hierarchical or multi-scale representations using p13x13t as building block.

Optimizable & Parameterized

Because of the “p,” you can parameterize how p13x13t blocks behave (weights, coupling, constraints).
The structure can be tuned for performance or compression.

Useful in Diverse Domains

As shown in use cases, p13x13t can be applied in image processing, machine learning, spatio-temporal modeling, cryptography, and more.

Challenges & Considerations in Using p13x13t

No framework is perfect. Here are some potential drawbacks or challenges:

Non-standard Dimension

Since 13×13 is not conventional (unlike powers of 2, e.g. 8×8 or 16×16), many libraries don’t support it natively.
Efficient transforms (e.g. fast Fourier or wavelet) may not have optimized routines for 13×13.

Memory & Computation Overhead

For large t (many time layers), storing many 13×13 matrices can grow expensive.
Computation per block might be heavier than for simpler units if transformations are complex.

Complexity of Parameters

Parameterizing coupling between cells, or defining boundary conditions, can introduce complexity.
Tuning parameters suitably for each use case might require significant experimentation.

Interfacing & Integration

If existing frameworks expect standard tensor shapes (e.g. powers of two), integrating p13x13t may require custom adapters.
Converting data to/from p13x13t structures may incur overhead.

Scalability Limits

For large systems, tiling too many 13×13 blocks might lead to inefficiency or edge artifacts.
Global coordination between blocks needs careful design.

Understanding ninawelshlass1: A Complete Guide

Implementation Strategy: How to Build with p13x13t

If you decide to experiment with p13x13t in your system, here is a roadmap to guide you.

1. Define the Use Case Clearly

Decide whether “t” is temporal, transform, or another dimension.
Decide what each 13×13 cell holds: scalar, vector, or structured data.
Define the operations you’ll need: read/write, interpolation, transform, update, merge.

2. Build a Basic Data Structure

Represent p13x13t as a 3D array: data[t][13][13].
Add metadata: timestamps, parameter settings, version numbers.

3. Implement Core Operations

Data access and update functions.
Interpolation between time slices (linear, spline, etc.).
Transform functions (e.g., 2D filter on each slice, cross-slice operations).
Merging or combining blocks (if tiling multiple p13x13t units).

4. Parameter & Configuration Module

Allow parameterization: coupling weights, boundary conditions, blend factors.
Provide default presets for common cases.

5. Performance Optimization

Use efficient low-level loops or vectorized libraries (e.g. NumPy, C++ arrays).
If many time slices, consider memory compression (sparse storage, delta encoding).
Parallelize operations across t slices or across cells.

6. Testing & Benchmarking

Validate correctness: check interpolation, transforms, merges.
Benchmark speed and memory usage compared to baseline approaches.
Test edge conditions: boundary behavior, missing data, extreme parameter settings.

7. Integration & API Exposure

Expose APIs (e.g. REST, RPC) to consume or produce p13x13t structures.
Provide converters to/from standard formats (e.g. plain images, tensors).
Document usage patterns and constraint rules.

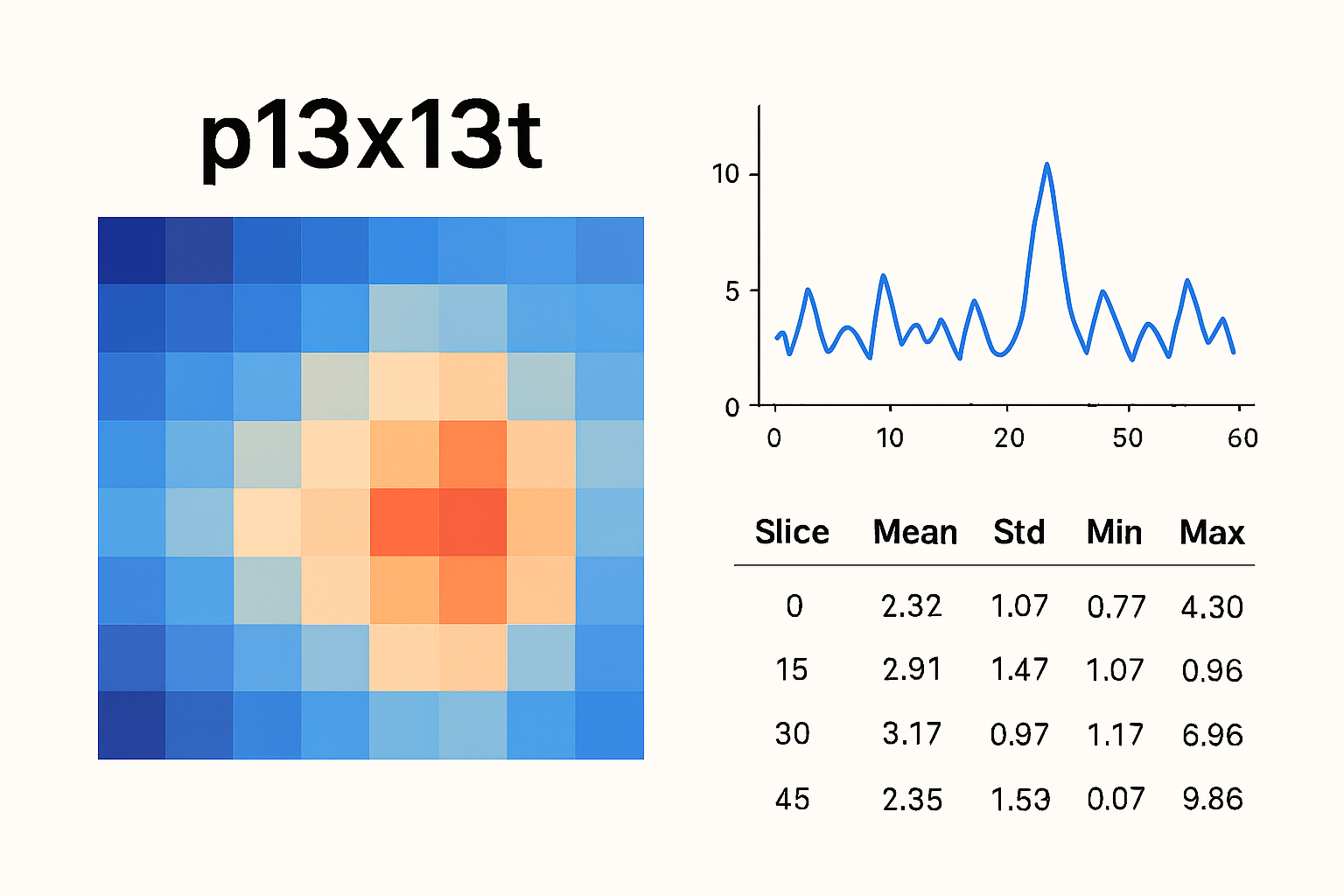
Example Walkthrough: p13x13t for a Sensor Grid

To make things more concrete, imagine you have a 13×13 sensor grid measuring temperature, and you collect readings every minute for 1440 minutes (a day). You want to model temperature evolution, detect anomalies, and forecast.

Structure: tempData[t][13][13] where t = 0..1439.
Parameterization: weight coupling between adjacent cells to smooth data, or penalize sudden changes.
Operations:
- Interpolate missing readings.
- Apply a spatial filter per time slice (e.g. 3×3 smoothing).
- Compute temporal derivative (tempData[t+1] − tempData[t]).
- Forecast next slice based on past slices and coupling parameters.
Analysis:
- Detect anomalies (e.g. a single cell deviating far from neighbors).
- Visualize the evolution (animations of the 13×13 grid).
- Compress data by storing only deltas or transformed coefficients.
Extension:
- Tile multiple p13x13t units to cover a larger region.
- Combine different modalities (e.g. sensor temperature + humidity) by having vector values in each cell.

This example shows how p13x13t can become a real tool in spatio-temporal modeling.

Best Practices & Tips for Working with p13x13t

Start small: Build minimal prototypes before full systems.
Use defaults first: Provide default parameters so users don’t need deep tuning initially.
Monitor metrics: Keep track of memory, compute time per block, error rates.
Document thoroughly: Because p13x13t is nonstandard, clear docs help adoption.
Provide adapter layers: Converters to/from common tensor shapes or image formats reduce friction.
Benchmark vs alternatives: Compare p13x13t against simpler matrices (e.g. 10×10, 16×16) to confirm advantage.
Modularize: Keep the p13x13t logic separate so you can replace or upgrade it later.
Graceful fallback: In cases where p13x13t is not optimal, allow switching to alternative structures.

Future Trends & Research Directions

Although p13x13t is speculative at present, several future directions look promising:

Standard Libraries & Toolkits
Developing open source libraries for p13x13t will encourage adoption. Support in major languages (Python, C++, Java) will reduce friction.
Efficient Transforms
Designing fast algorithms (FFT-like) for 13×13 transforms could unlock high performance.
Nonlinear Extensions
Introduce nonlinearity across slices (t dimension) or within the grid (e.g. cell coupling that changes over time).
Machine Learning Integration
Use p13x13t blocks as building units in neural architectures (e.g. convolutional networks with 13×13 kernels evolving over t).
Compression & Encoding
Explore compressing p13x13t data (delta coding, quantization) for storage and transmission efficiency.
Adaptive Schemes
Let the dimension adapt (e.g. sometimes 13×13, sometimes 13×N) based on data characteristics, or grow/shrink grid size dynamically.
Quantum & High Performance Computing
Investigate whether p13x13t structures map well to quantum circuits or GPU architectures.

Limitations & Cautionary Notes

Because p13x13t is nonstandard, adopting it comes with risk: lack of tooling, community support, and unknowns.
Always validate that the added complexity yields real benefits (performance, expressiveness) over simpler models.
Be cautious about memory/time blowup when t becomes large or when tiling many blocks.
Edge effects when combining blocks need careful handling to avoid seams or artifacts.
Data compatibility: ensure that you can map existing data into and out of p13x13t without losses or distortions.

Conclusion

In summary, p13x13t is a compelling conceptual framework that centers on a 13×13 matrix structure extended over a “t” dimension (time, transform, or other layering), with parameterized flexibility. Though it is not yet a widely recognized standard, it offers interesting tradeoffs: manageable complexity, temporal dynamics, modularity, and expressive potential.

We explored:

Its theoretical foundation (why 13×13, what “p” and “t” might mean)
Core architecture and design
Use cases across image processing, machine learning, sensor networks, cryptography, and games
Benefits (balanced complexity, composability, parameterization)
Challenges (nonstandard dimension, overhead, integration difficulty)
Implementation roadmap and best practices
Example scenario (sensor grid)
Future directions and research possibilities
Limitations and cautions

Niggsymac: A Deep Dive into a Unique Digital Identity

FAQs About p13x13t

1. What is p13x13t?
p13x13t refers to a structured 3D data model or grid composed of 13×13 spatial dimensions across multiple time steps. It’s often used in computational modeling, AI simulations, or spatial-temporal data analysis.

2. What are the main uses of p13x13t?
p13x13t can be used in areas like image processing, scientific research, anomaly detection, and digital signal analysis. It helps researchers visualize and analyze how data changes over time within a fixed 13×13 grid.

3. Is p13x13t a software or a concept?
It’s primarily a data structure concept, but it can be implemented in programming environments like Python, MATLAB, or R using 3D arrays and numerical tools.

4. How does p13x13t differ from a normal 2D matrix?
A standard 2D matrix handles spatial data in two dimensions (rows and columns). p13x13t adds a third dimension — time — allowing you to track dynamic changes or movement across frames.

5. Can beginners work with p13x13t?
Yes. Beginners with a basic understanding of Python or data arrays can easily experiment with p13x13t using libraries like NumPy or Matplotlib for analysis and visualization.

6. What is the purpose of the 13×13 grid size?
The 13×13 grid is a standard or symbolic size that balances resolution and computational efficiency. It’s large enough to hold meaningful data patterns but small enough for quick calculations.

7. Can p13x13t be used in machine learning?
Absolutely. p13x13t data can feed into machine learning models for pattern recognition, prediction, or anomaly detection, especially in time-series or image-sequence tasks.

8. How can I visualize p13x13t data?
You can visualize it as a sequence of 13×13 heatmaps, animations, or 3D volume plots. Tools like Matplotlib, Plotly, or Seaborn in Python are ideal for this.

9. What are the advantages of using p13x13t?
It offers compact data representation, clear temporal insights, and easy adaptability for AI or data science applications. It’s especially useful for analyzing small dynamic systems efficiently.

10. Where can I learn more about p13x13t?
You can explore tutorials and documentation on numerical computing, data visualization, or custom data structure modeling — most of which are freely available on educational platforms and GitHub.

Table of Contents